Haus bauen leicht gemacht
Der moderne Hausbau ist mehr denn je zu einem Symbol für Verwurzelung und Selbstverwirklichung geworden. Doch was ist zu beachten, wenn der Wunsch nach dem Eigenheim erst einmal formuliert ist?
Vom Grundstückskauf über die verschiedenen Planungsphasen können im Folgenden alle wichtigen Informationen zum Thema Haus bauen detailliert abgerufen werden.
- Nützliche Informationen für Ihr Bauprojekt
- Unterstützung bei der Finanzierungsplanung durch unseren Hauskreditrechner
- Aktuelle Hauskredit Zinsen und Kreditangebote
Haus bauen: Grundstückskauf, Baugenehmigung und Kosten
Wer über das den Hausbau nachdenkt, ist auf ein geeignetes Baugrundstück angewiesen. In aller Regel wird es beim Hausbauen Auflagen der Gemeinde zu Gebäudegröße, Dachgestaltung und dergleichen zu beachten geben. Hier ist nicht automatisch erlaubt, was der Nachbar schon gebaut hat.
Auch die Grundstückspreise unterscheiden sich in den Regionen zum Teil stark und sollten vorab ermittelt und in die Kalkulation der Kosten eingestellt werden.
Der Hausbau in vertrauensvollen Händen
Die Übertragung der Planungs- und Bauleistungen in verantwortungsvolle Hände gehört zum A und O, wenn man ein Haus bauen möchte. Kann man sich auf die beauftragten Firmen verlassen, wird das Projekt ein Erfolg. Hier stehen Interessenten verschiedene Möglichkeiten zur Verfügung, ihr Haus zu bauen:
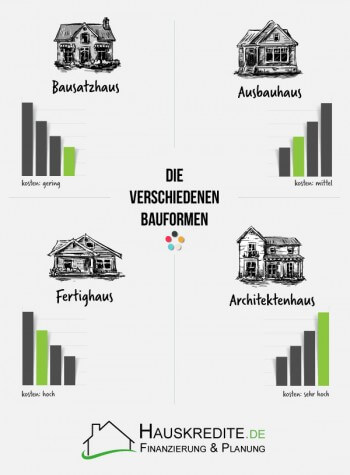
Haus bauen: Die verschiedenen Bauformen
Beim Bausatzhaus übernimmt der Bauherr den höchsten Grad an Eigenleistung, kann parallel aber das meiste Geld sparen.
Mit handwerklichem Geschick, einem großen und ebenfalls geschickten Freundeskreis und entsprechend viel Freizeit, kann der Traum ein Haus zu bauen hier mit deutlich geringeren Ausgaben wahr werden. Die Ersparnis wird in der Regel aber auf Kosten der Zeit gehen und die Bauphase um ein Vielfaches verlängern.
Ein Ausbauhaus lohnt sich für Bauherren, die beim Haus-Bauen zwar gern Eigenleistungen übernehmen und somit bares Geld sparen wollen, die jedoch keine Rohbauarbeiten leisten wollen, wie sie beim Bausatzhaus abverlangt werden.
Doch auch hier gilt, wer sein handwerkliches Geschick, die zur Verfügung stehende Zeit oder die eigene Energie überschätzt, zahlt am Ende unter Umständen drauf.
Das Fertighaus oder Fertigteilhaus stellt die häufigste Bauform beim Haus-Bauen dar. Die besonders aufwendigen Aufgaben und Herausforderungen der Bauleitung können hier an einen Profi übertragen werden, der in aller Regel auch die Gewährleistung übernimmt.
Besonders in der Gegenüberstellung von Kosten und Verantwortlichkeiten des Bauherren zeigen sich die großen Vorteile des Fertighausbaus. Vorsicht ist jedoch besonders bei der Vertragsgestaltung geboten - nicht jedes schlüsselfertige Haus entspricht den Vorstellungen vom eigenen Traumhaus.
Das Architektenhaus bietet neben der individuellen Gestaltung des Gebäudes auch ein hohes Maß an Entspannung für den Bauherren.
Der Architekt übernimmt nicht nur die reine Planung des Hausbaues, er überwacht auch die Bauarbeiten, koordiniert die Gewerke und vermittelt zwischen den Vertragsparteien. Im Gegenzug sollte der Bauherr klare Vorstellungen von seinem künftigen Gebäude und ein Gespür für angemessenes Architekten-Honorar haben.
Ein Niedrigenergiehaus ist für alle diejenigen genau das Richtige, die auf eine energiesparende Lebensweise und umweltverträgliche Bauweise bedacht sind.
Zwar sind die Baukosten durch das Nutzen von ökologischen Baumaterialien anfangs höher als im Vergleich zur konventionellen Bauweise. Die Mehrkosten amortisieren sich jedoch durch die hohen Einsparungsmöglichkeiten beim Energieverbrauch.
Das Modulhaus bietet durch den Bau mit Modulteilen den großen Vorteil, dass die Bauarbeiten schnell und günstig abgeschlossen werden können. Auch eine Erweiterung oder Verkleinerung der Wohnfläche ist bei dieser Bauweise unkompliziert möglich.
Durch eine spezielle, umweltfreundliche Bauweise herrscht von Anfang an ein gutes Raumklima. Allerdings muss man berücksichtigen, dass hier keine Unterkellerung möglich ist.
Das Containerhaus hat durch seine kostengünstige Bausweise den großen Vorteil, dass sich auch Bauherren mit nur kleinem Budget den Traum vom Eigenheim verwirklichen können.
Allerdings müssen gewisse Abstriche bei den Isolierungsmöglichkeiten einige Abstriche gemacht werden. Ein großer Vorteil ist allerdings das hohe Maß an Flexibilität, wenn etwa eine Vergrößerung notwendig wird.
| Bauform | Kosten | Eigenleistung | Individualität |
|---|---|---|---|
| Bausatzhaus | gering | sehr hoch | in der Gestaltung sehr hoch |
| Ausbauhaus | mittel | hoch | innen sehr hoch |
| Fertighaus | hoch | mittel bis gering | gering |
| Architektenhaus | sehr hoch | mittel bis gering | insgesamt sehr hoch |
| Niedrigenergiehaus | (sehr) hoch | mittel bis hoch | mittel bis hoch |
| Modulhaus | gering | gering | in der Gestaltung sehr hoch |
| Containerhaus | gering | gering | gering |
Alles zum Thema Haus bauen
D
F
H
S
Haus bauen: Baustoffe und Energiestandards
Wer einen Hausbau plant, sollte sich möglichst frühzeitig über die gewünschten Baustoffe informieren. Zur Wahl stehen neben Holz und Ziegel auch moderne Betonfertigteile, Hohlsteine oder Mischformen.
Jeder Baustoff hat seine eigenen bauphysikalischen Vor- und Nachteile, verursacht unterschiedlich hohe Kosten und setzt ganz verschiedene Wandstärken voraus. Hier lohnt sich der genaue Blick auf die Möglichkeiten, denn je nach Materialwahl, können teils lohnende Fördermittel beantragt werden.
Fenster, Türen, Fassade und Dach - "Haus bauen" im Detail
Die Gebäudehülle samt Fenstern und Türen ist das Aushängeschild eines jeden Hausbau-Projekts. Materialeinsatz und Farbauswahl können hier darüber entscheiden, ob Bauherr und zufälliger Betrachter ein Gebäude als schön empfinden oder nicht.
Im Laufe des Planungsprozesses muss entschieden werden, welchen Stellenwert hier Optik und Energieeffizienz bekommen - beides beeinflusst am Ende direkt das Erscheinungsbild des Hauses und entscheidet über den langfristigen Erfolg des Projekts.
Technische Anlagen - Herausforderungen beim Hausbau
Das Thema Hausbau war noch nie so eng mit Fragen zu Energieeffizienz, Wahl der Heizungsform, Stromerzeugung und Warmwasserbereitung verknüpft, wie heute.
Ausgaben für die technischen Anlagen nehmen im modernen Hausbau gern einmal ein Drittel der Gesamtbaukosten ein.
So ist es nicht ungewöhnlich, dass Bauherren sich mit den technischen Anlagen besonders lang und intensiv beschäftigen. Auch hier sind Fördermittel zum energieeffizienten Hausbau ein Kriterium, das beachtet werden sollte.
Außenanlagen - Thema "Haus bauen" betrifft auch den Garten
Schon bei den ersten Überlegungen zum Hausbau spielt die Gartengestaltung eine wichtige Rolle. Die Außenanlagen umfassen dabei sowohl den künftigen Rasen, als auch sämtliche befestigte Bereiche der Zufahrt, der Wegeverbindungen und Garagen.
Bauherren müssen beim Bauen eines Hauses frühzeitig auf ihr Budget achten - nur allzu gern fallen unerwartete Zusatzkosten dem Außenanlagenbudget zur Last.
Darüber hinaus sind bei der Errichtung von Garagen, Carports und Gartenhäuschen, aber auch bei der Pflanzung von Gehölzen die entsprechenden Vorgaben der Landesbauordnung zu beachten. Berücksichtigt man die rechtlichen Vorgaben, kann das Projekt Hausbau zum ganz großen Abenteuer werden.
Einzelnachweise
Mannek, Wilfried: Hausbau in Eigenleistung »
Stimpel, Roland: In 10 Schritten zum Eigenheim »

 Kreditvergleich
Kreditvergleich  Hauspreis Rechner
Hauspreis Rechner  Hauskauf Nebenkosten
Hauskauf Nebenkosten 